2023
Gold leaf on raised gesso, handmade gum tempera and shell gold on cotton rag paper
58.5 x 43.5 cm
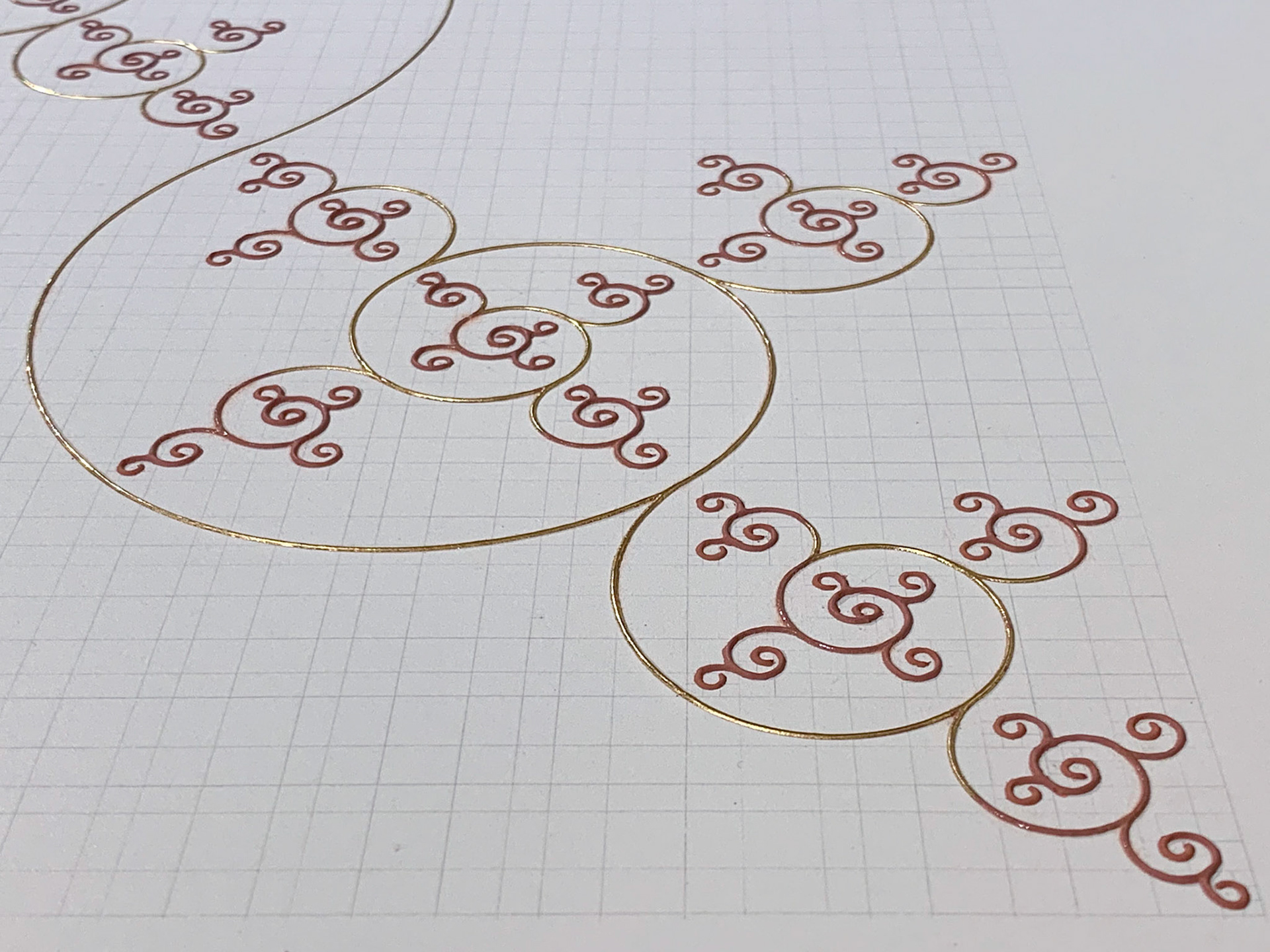
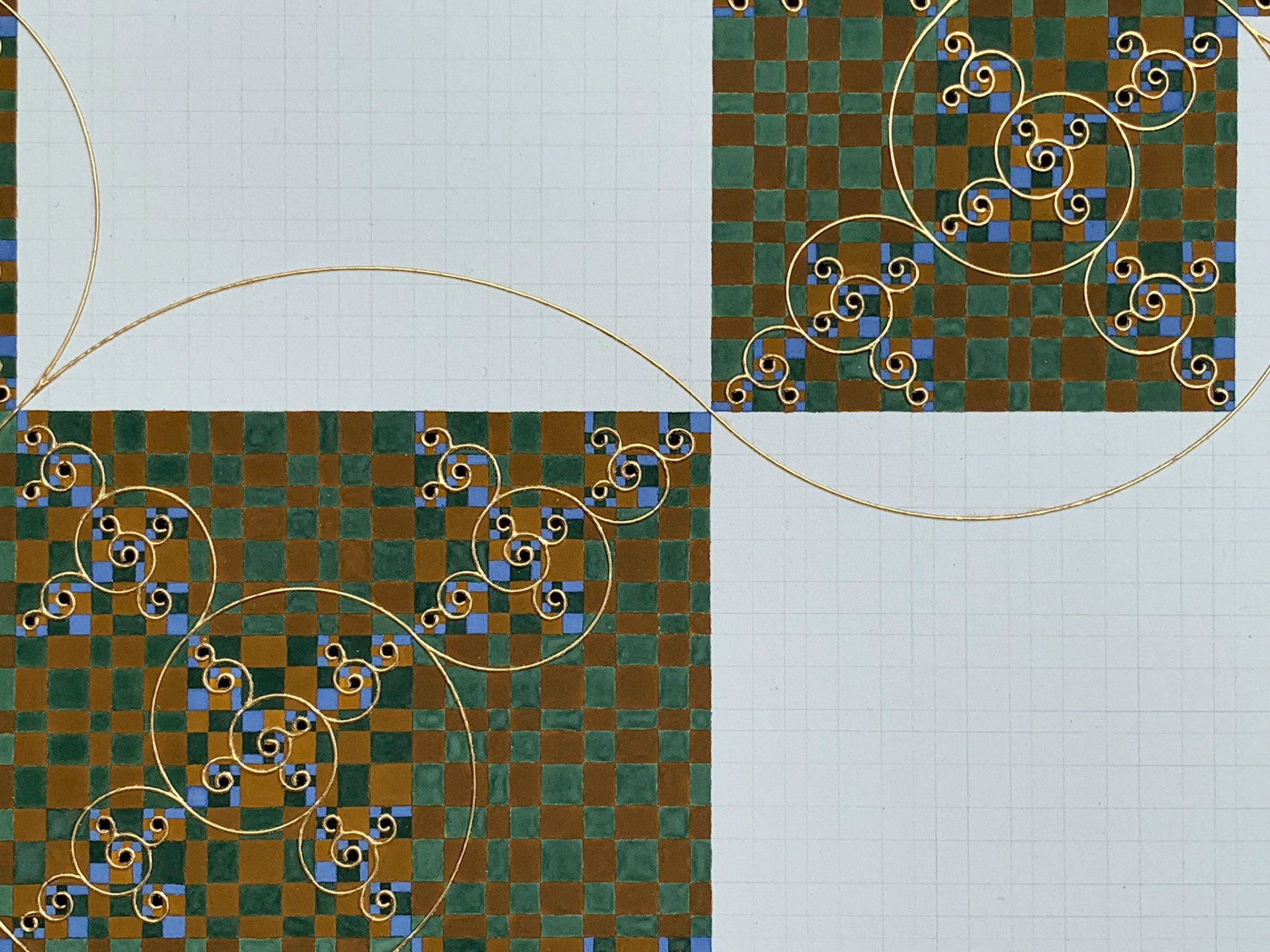
This is the first piece in a series where I explore fractal curves using the technique of diapering from European manuscript illumination, inspired by the work of British mathematician Edmund Harriss. Most people are familiar with the golden rectangle and the spiral that can be constructed in it, but this is only one example of a more general idea of how a rectangle can be divided into squares and rectangles. The solutions in all cases are algebraic and the golden ratio is just one of them. By applying this method of division to other proportional rectangles, Harriss arrived at his ‘proportion systems’ and discovered a new fractal spiral that now bears his name.
But like its golden cousin, the Harriss Spiral is also governed by an irrational number, in this case the plastic ratio, making it impossible to tile the rectangle with whole multiples of the diapering unit — if it is possible to construct a plastic rectangle with traditional straight edge and compass at all!
My solution is to approximate the plastic rectangle using the “whirling squares” method. Very much like we can get ever closer to the golden rectangle by building a spiral of squares with side lengths in Fibonacci sequence, I built up my rectangle with a spiral of squares with sides in Padovan sequence. The size of the first and smallest squares in the spiral then sets the unit size for the diapering pattern.
From the iteration of simple steps, complex patterns emerge.